Ce sujet sera traité sur l’exemple de la représentation des protéines en science, et de la contribution de Jane Richardson, une biophysicienne dont l’expertise pour la recherche graphique a marqué durablement l’histoire de la science. Tout au long de cet article seront proposés un certain nombre de rappels pour faciliter la compréhension de tous, à tout niveau.
Préambule : quelques notions de bio pour avoir toutes les clefs en mains pour comprendre cet article !




Introduction : Jane, c’est qui ?

Je vais commencer cet article en m’émerveillant un peu de la contribution de Jane Richardson dans la recherche. Ses articles affichent un total de citations supérieur à 73 850, dont plus de 33 246 depuis 2017. Le nombre de fois qu’un auteur est cité est un bon indicateur de l’impact de ses travaux, qui se sont avérés utiles pour nombre de scientifiques. Au total, une cinquantaine d’articles scientifiques, étalés entre 1967 (Jane avait alors 26 ans) et 2022.
…A titre de comparaison purement risible – et entre Jeanne –, j’ai 27 ans, 4 articles à mon actif pour un total de… 9 citations !
Son article le plus cité est PHENIX : a comprehensive Python-based system for macromolecular structure solution, cité 20670 fois, publié dans le journal scientifique Acta Crystallographica Section D en 2010 et pour lequel Jane est co-auteure.
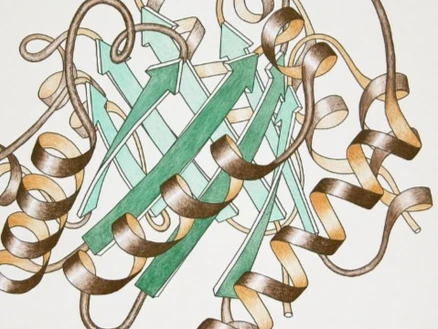
Jane fait partie des pontes qui ont mis au point la convention désormais mondialement utilisée de représentation des protéines : le modèle ruban. Aujourd’hui nous représentons les protéines selon ce modèle de manière tellement évidente que nous oublions qu’il a été mis au point grâce à des recherches graphiques essentielles à la communication scientifique. Un bel exemple du caractère nécessaire de l’art en science, bien loin du but purement décoratif. C’est ce que je vous propose de voir aujourd’hui : comment, sans l’art – sans représentations graphiques, visuelles – nous nous retrouvons bloqués dans nos avancées scientifiques et dans notre compréhension de la science.
1 – Comment la mise au point d’un modèle visuel de représentation des protéines s’est révélée être une nécessité ?
a) Le premier modèle
Alors que la structure de l’ADN est connue depuis 1953, celle des protéines ne l’est toujours pas.
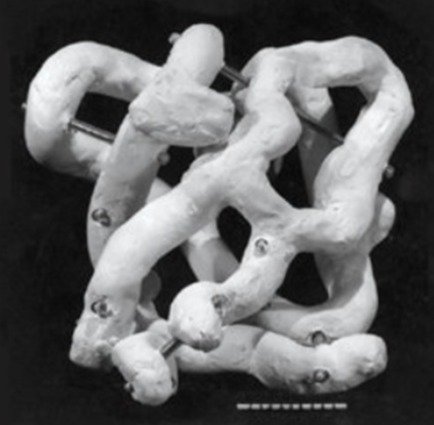
En 1957, le biochimiste John Kendrew propose le tout premier modèle explicatif de la structure des protéines : le très vendeur modèle « saucisse » (cf image), en prenant pour exemple la myoglobine, une protéine de type globine (on l’aura deviné) et contenant un atome de métal (le fer). Elle est présente dans le cytoplasme des cellules musculaires des vertébrés et plus particulièrement des mammifères, et stocke du dioxygène.
Mais le modèle saucisse n’est pas convaincant. John lui-même critique ce modèle, qui ne met en évidence aucune règle de repliement des protéines.
b) Les images scientifiques brutes obtenues de l’étude des protéines
Etudier la structure des protéines est une discipline à part entière – d’ailleurs toujours d’actualité – et qui porte le doux nom de cristallographie. Dès les années 1960, les cristallographes accumulent des données de structures de protéines par cristallographie aux rayons X (cf images).


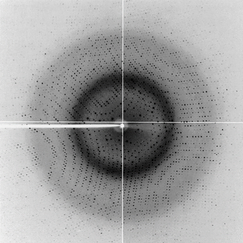
Ci-dessus sont des images de diffraction d’un cristal de protéine obtenues par diffraction des rayons X. Chaque point noir représente une tache caractéristique de l’emplacement d’un des atomes qui constituent le cristal de la protéine observée.
c) Le problème
Mais les cristallographes se heurtent à deux difficultés majeures : comment comparer facilement deux protéines entre elles à partir de ces images et comment expliquer le repliement des protéines à partir de la structure primaire ?
Pour surmonter ces obstacles, il leur manquait deux éléments essentiels :
– Des outils de comparaison pour révéler des ressemblances entre les différentes structures obtenues et pouvoir alors les classifier : devait alors naître la taxonomie des protéines.
– Un mécanisme permettant d’expliquer le processus de repliement des protéines, encore incompris. A cette époque, il était déjà admis que la forme fonctionnelle d’une protéine (appelé état natif) correspond à un minimum d’énergie, c’est-à-dire que la protéine est stable. Mais comment la protéine parvenait à aboutir à cette conformation stable ? L’hypothèse de l’essai-erreur aboutissant à la bonne conformation par un processus aléatoire ne permet pas un repliement aussi rapide que celui observé. Restait donc à découvrir les mécanismes sous-jacents.
2 – Développement du modèle de représentation des structures secondaires
a) Dessiner les structures secondaires pour les comparer
Pour comprendre les mécanismes de repliement des protéines, il a déjà fallu comprendre que la structure tridimensionnelle des protéines dépend de l’organisation des structures secondaires entre elles. La structure secondaire a été étudiée simultanément par l’équipe de Michael Levitt et Cyrus Chothia d’une part (1976) et par Jane Richardson d’autre part (1977). Pouvoir visualiser l’organisation de ces structures était donc devenu le point névralgique de ces travaux. Plusieurs topologies ont alors été proposées pour visualiser les structures des protéines et simplifier le problème de repliement. Parmi ces topologies, celle de la clef grecque proposée par Jane Richardson a été celle qui a rencontré le plus de succès pour représenter les feuillets bêta.

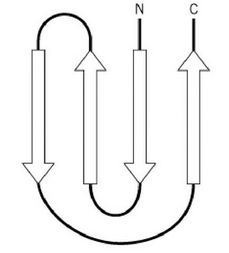
Différentes classifications ont alors pu rapidement vu le jour (Richardson 1981, Rossmann et Argos 1981). Dessiner les topologies a donc enfin permis de comparer les structures secondaires et donc classifier les protéines !
b) L’enjeu : trouver une représentation compréhensible immédiatement
Le problème de représentation de la structure tridimensionnelle des protéines persistait en effet, puisque le modèle saucisse proposé par Richard Dickerson en 1969 restait peu satisfaisant.
Ci-dessous sont des représentations de protéines par Richard, et qui laisse assez obscure la compréhension des détails de la structure de ces protéines :

Ce qui était recherché, c’était une représentation permettant une compréhension immédiate des structures des protéines et une comparaison simple des différentes structures entre elles. Jane Richardson conduit plusieurs tentatives, présentées ci-dessous, par des figures présentés dans des articles co-écrits par Jane.
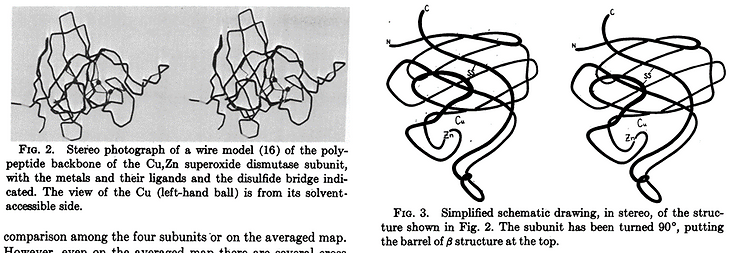

Il est intéressant de prendre conscience à quel point la représentation graphique d’une entité invisible à l’œil nu et à forme abstraite nécessite de la recherche, au même titre que la compréhension de modèles scientifiques nécessite de la recherche. Cette approche met en évidence l’importance de considérer l’art comme un outil scientifique, au service de la réflexion, de la compréhension et de la communication.

3 – De la compréhension de l’impact de nos recherches jusqu’à l’art de la communication pour généraliser un modèle
a) Encore faut-il comprendre l’impact de notre découverte !
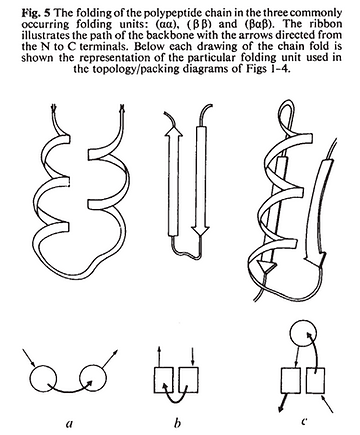
Le modèle ruban voit enfin le jour, proposé pour la première fois par Michael Levitt et Cyrus Chothia (1976) et publié dans le très fameux journal scientifique d’experts, Nature.
Mais la recherche graphique sur ce dessin reste pauvre, si bien que Levitt et Chothia n’insistèrent pas sur le caractère innovant de cette représentation. A tel point qu’ils l’ont abandonné ! Au profit de modèles plus abstraits, comme nous pouvons le découvrir dans leur article publié l’année suivante, dans lequel le modèle ruban n’est plus du tout présent, et où seul le modèle en petits cercles et de feuilles plissées subsiste (voir ci-dessous).
En effet, il ne suffit pas de découvrir des choses révolutionnaires… Encore faut-il pouvoir comprendre l’envergure de nos découvertes sur le monde.
Levitt et Chothia n’ont pas été les seuls scientifiques à passer à côté de leur propre impact sur le monde de demain, Beink aura l’occasion de vous en présenter d’autres exemples dans son blog.
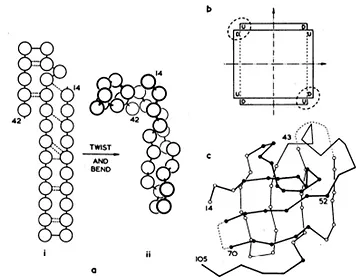
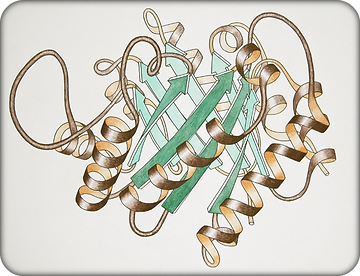
C’est Jane Richardson qui a immédiatement saisi l’intérêt du modèle ruban.
Elle l’a adopté, y a introduit des couleurs de manière stratégique, permettant ainsi de faciliter la distinction entre les différents motifs, et l’a présentée dans une affiche en 1979. Ses illustrations, publiées dans ses différents articles, sont même reprises par d’autres chercheurs pour leurs propres publications.
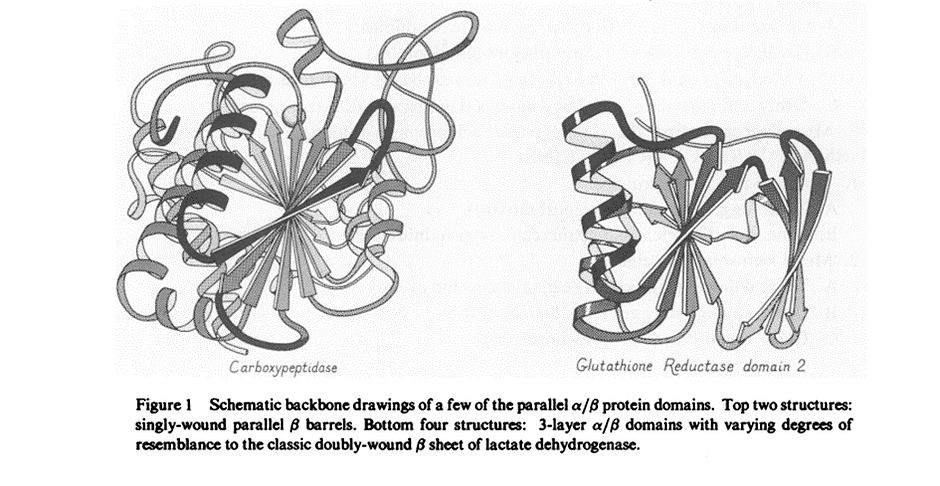
L’impact de cette nouvelle représentation, accompagné de la description de ses avantages, a été immédiat.
b) Une découverte doit être présentée selon les bons codes pour être comprise
Il ne suffit pas de jeter un résultat à la figure de ses lecteurs et d’attendre qu’ils comprennent tout seuls son importance.
L’accueil à bras ouvert du modèle ruban tel que l’a présenté Jane Richardson ne sort pas de nulle part ! Car en plus de comprendre l’importance d’une découverte, il faut aussi savoir la valoriser et la présenter à son public. Une bonne représentation et mise en valeur permet à tous de comprennent en quoi une découverte est révolutionnaire.
Cette règle de « savoir publier » est toujours au goût du jour, puisque que lorsque nous apprenons à rédiger un article scientifique on nous demande de raconter une histoire, d’amener le lecteur tout du long de notre argumentation jusqu’à ce que la conclusion de notre résultat lui paraisse irréfutable. Une méthode de communication qui s’applique bien plus largement qu’au seul domaine scientifique bien sûr.
c) Généralisation du modèle ruban par-delà les frontières
Le modèle ruban a ensuite été rapidement adopté par les différents scientifiques à travers le monde.
Mais la recherche graphique ne s’arrête pas là : Jane Richardson passe deux années supplémentaires à améliorer le modèle ruban, motivée par plusieurs axes de recherche, dont :
– Comprendre les relations évolutives entre les protéines, grâce à des représentations qui révèlent les ressemblances de façon immédiate.
– Démontrer que la représentation des données est un travail d’importance égale avec l’accumulation des données (la représentation des données est aujourd’hui une discipline connue sous le nom de Data Visualisation, présentée dans l’article de blog Beink suivant : cliquez ici)
– L’esthétique des formes et les points communs qu’elle pouvait mettre en évidence avec des motifs existants tels que la clef grecque.
Six ans après la première représentation à main levée du modèle ruban par Jane, un algorithme voit le jour permettant de générer des protéines selon cette représentation, mis au point par Mike Carson (Carson, 1986). On oublie aujourd’hui que ce n’est pas l’algorithme qui est à l’origine de cette représentation ! Celui-ci a permis aux scientifiques de générer des structures protéiques non plus à la main mais numériquement, participant amplement à la généralisation du modèle.
Pour conclure…
L’interdisciplinarité, une ressource intellectuelle essentielle aux grandes avancées
Les compétences de réflexion en graphisme de Jane Richardson, couplée à sa compréhension extrêmement fine et profonde de son domaine scientifique, semblent puiser leurs sources dans le parcours varié et interdisciplinaire de cette grande scientifique.
Jane a commencé ses études supérieures dans le domaine de la philosophie avant de prendre un tournant radical vers la chimie des protéines et la caractérisation de leurs structures. Jane a sans aucun doute mis à contribution ses compétences philosophiques au service de la science dans la construction, l’élaboration et la communication du modèle ruban que nous utilisons tous désormais.
Ce qui est particulièrement remarquable, c’est que 30 ans après l’apparition du modèle ruban, la manière de représenter les protéines reste inchangée malgré l’énorme progrès des connaissances dans la compréhension des mécanismes par lesquels les protéines assurent leurs fonctions. Par ailleurs, cette représentation s’est révélée particulièrement adaptée à deux nouveaux sujets de recherche qui ont émergé dans les années suivantes : la conception de protéines artificielles et la description des mouvements internes des protéines impliqués dans le fonctionnement de ces nanomachines.

En 2011, dans son article intitulé « Construction of the ribbon model of proteins, The contribution of Jane Richardson » (Morange, 12011), qui retrace l’historique de l’établissement du modèle ruban, Michel Morange nous transmet son message très à-propos : « l’importance des représentations dans le travail scientifique est souvent sous-estimé ».
Références :
Google Scholar :
– publications de Jane Richardson
– publications de Jeanne Le Peillet
Articles :
ADAMS, Paul D., AFONINE, Pavel V., BUNKÓCZI, Gábor, et al. PHENIX: a comprehensive Python-based system for macromolecular structure solution. Acta Crystallographica Section D: Biological Crystallography, 2010, vol. 66, no 2, p. 213-221.
CARSON, Mike et BUGG, Charles E. Algorithm for ribbon models of proteins. Journal of Molecular Graphics, 1986, vol. 4, no 2, p. 121-122.
CHOTHIA, Cyrus, LEVITT, Michael, et RICHARDSON, Douglas. Structure of proteins: packing of alpha-helices and pleated sheets. Proceedings of the National Academy of Sciences, 1977, vol. 74, no 10, p. 4130-4134.
DICKERSON, G.E. (1969). Experimental approaches in utilizing breed resources. Anim. Breed. Abstr., 37: 191–202.
LEVITT, Michael et CHOTHIA, Cyrus. Structural patterns in globular proteins. Nature, 1976, vol. 261, no 5561, p. 552-558.
LOW, Barbara W., PRESTON, Hugh S., SATO, Atsushi, et al. Three dimensional structure of erabutoxin b neurotoxic protein: inhibitor of acetylcholine receptor. Proceedings of the National Academy of Sciences, 1976, vol. 73, no 9, p. 2991-2994.
MORANGE, Michel. What history tells us XXV. Construction of the ribbon model of proteins (1981) The contribution of Jane Richardson. Journal of biosciences, 2011, vol. 36, no 4, p. 571-574.
RICHARDSON, Jane S., RICHARDSON, D. C., TWEEDY, N. B., et al. Looking at proteins: representations, folding, packing, and design. Biophysical Society National Lecture, 1992. Biophysical journal, 1992, vol. 63, no 5, p. 1185.
RICHARDSON, Jane S., TAINER, John A., et RICHARDSON, David C. An illustrated museum of protein structures. Biophysical journal, 1980, vol. 32, no 1, p. 211.
RICHARDSON, J., THOMAS, Kenneth A., RUBIN, Byron H., et al. Crystal structure of bovine Cu, Zn superoxide dismutase at 3 A resolution: chain tracing and metal ligands. Proceedings of the National Academy of Sciences, 1975, vol. 72, no 4, p. 1349-1353.